Winstgevend handelen.

04-01-2016.
Ik wilde deze verzameling van stukjes die ik de komende tijd ga schrijven eerst noemen 'Het opbouwen van een handelssysteem'.
Maar daar heb ik vanaf gezien, het wordt dus: 'Winstgevend handelen'.
Om winstgevend te kunnen handelen volstaat het echt niet om met bijvoorbeeld slechts één indicator te werken.
Diegene die zeggen dat wel te doen, en ook winst maken, gebruiken vaak meer indicatoren/ideeën dan dat ze wellicht zelf in eerste instantie doorhebben.
Wat zijn de basis bouwstenen waarmee je moet werken om winstgevend te kunnen handelen.
Ik denk dat daarin minimaal het volgende op één of andere wijze verwerkt moet zijn.
 1. Het rekening houden met overbought en oversold levels
 2. Trend detectie
 3. Kijk naar de markt in zijn geheel, broad market integration
 4. Steun en weerstand levels
 5. Historical volatility
 6. Implied Volatility
 7. Projected Implied Volatility
 8. Analyse over meerde tijdframes.
Nu zult u wellicht zeggen/denken:  daar hebben we al een enorm arsenaal aan indicatoren voor beschikbaar; en dat klopt.
Echter veel van die indicatoren komen uit de vorige eeuw.
In die tijd was de handel -anders-.
Sinds ruwweg het jaar 2000 / 2002 is de handel in opties en andere afgeleidde producten enorm toegenomen.
Sinds die tijd hebben we een grote toename gezien van hedgefunds en ook de 'grote jongens' handelen meer in opties e.a. dan in de aandelen zelf.
Dat de handel gewijzigd is van het kopen van aandelen naar de handel in opties blijkt wel uit de volgende grafiek:
[b][u]Grafiek 1:[/u][/b]
http://www.jstas.com/DJIA-volume.png

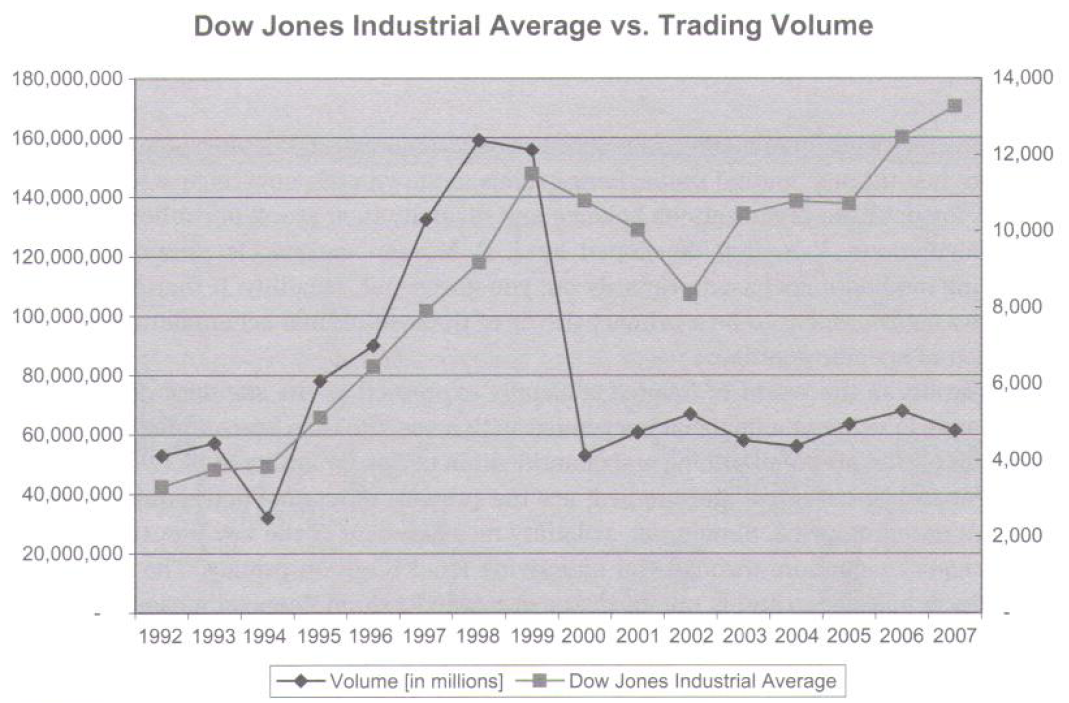
Bron: data uit Reuters QuoteCenter
U ziet dat terwijl de koers van de Dow Jones verder stijgt, het volume van het aantal verhandelde aandelen enorm is gedaald.
Kijken we naar het aantal optie contracten dan zien we dat dit gestegen is.
[b][u]Grafiek 2:[/u][/b]
http://www.jstas.com/Opt-volume.png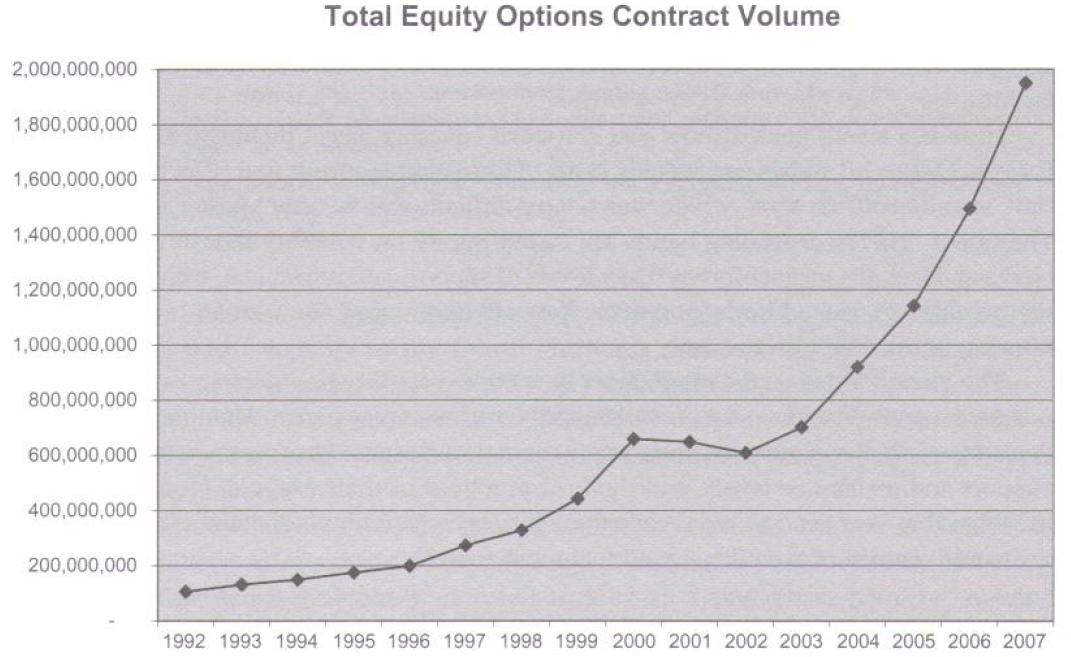

Bron: Chicago Board Options Exchange, 2007 Market Statistics Report.
Een verschuiving van het aantal verhandelde aandelen naar het aantal optie contracten.
De handel in opties e.a. is dus enorm toegenomen sinds 2000-2002, en het zijn de 'grote - jongens' die uiteindelijk de prijs bepalen, die paar opties of aandelen van mij zijn niet merkbaar in het geheel.
Die grote jongens werken natuurlijk met systemen (handelssystemen als je dat zo wil noemen) en die zijn niet uitgedacht door de eerste de beste die het basis onderwijs verliet ;)
Wanneer je hun vacature sites bekijkt zie je salarissen die in de tonnen lopen.
En, denk er eens even over na, verwacht je dat die 'grote - jongens' tonnen aan salarissen gaan betalen aan mede werkers die de hele dag een Fibonacci lijntjes trekken of een retracement uitrekenen?
Niet natuurlijk, hun systemen / algoritmes proberen signalen in de grafiek naar voren te brengen die zo voor het blote oog niet zichtbaar zijn.
Verder zijn hun systemen natuurlijk meer dan normaal er op ingesteld om zoveel als mogelijk is risico te mijden, de eerste winst ligt immers in het gegeven geen verlies te maken.
En omdat de grote jongens nu eenmaal -de koers-  bepalen zullen we om -winstgevend te handelen-  onze wijze van handelen daarop af moeten stellen.
Dat betekent dat we onze indicatoren (voor zover mogelijk) moeten gaan aanpassen voor detectie van signalen die in de optie handel voorkomen.
En dat wil ik komend jaar voor u proberen neer te gaan zetten.
Ik wil de komende periode eerst eens beginnen met iets heel gemakkelijks, het bepalen van de trend.
U kent wel het gezegde: 'handel niet tegen de trend want dan verdien je geen cent' ;)
Maar is het bepalen van de trend wel zo eenvoudig?
Daarover gaat het eerst volgende hoofdstukje.
Later gaan we in op de andere punten hierboven genoemd.
Ik ben niet zo slim, ik haal mijn kennis uit de markt en ik zal proberen zoveel als mogelijk is mijn bronnen te vermelden zodat u e.e.a. zelf kan nalezen/kijken.
..
[b][u]De trend.[/u][/b] 21-02-2016
Vraag aan twee handelaren wat de trend is, en wanneer de één zegt dat de trend omlaag is en de ander zegt dat de trend omhoog is dan kunnen ze allebei gelijk hebben.
Dat komt omdat de vraagstelling eigenlijk al onjuist is en het antwoord niet compleet.
Bij de vraag wat de trend is hoort eigenlijk ook de vermelding over welke tijd je dat wilt weten.
Bekijken we eens een theoretisch stukje koersgrafiek, zie grafiek 3.
[b][u]Grafiek 3:[/u][/b]
http://www.jstas.com/Trend1.png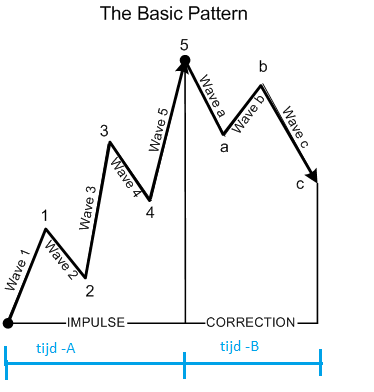

In grafiek 3 ziet u het basis patroon van de Elliott wave telling.
Gedurende tijd -A zien we hogere bodems en hogere toppen, en een analist die tijd A bekijkt zal spreken van een stijgende trend.
Gedurende tijd -B zien we een lagere top en een koers die onder de voorgaande bodem gaat en een analist die dat tijdtermijn bekijkt zal spreken van een dalende trend.
Maar in tijd -A zien we stukjes dalende en stijgende trend.
Om kort te gaan, bij de vraag wat is de trend hoort ook vermeld te worden wat het tijdsbestek is waar over wordt gekeken.
.
Wanneer we een stuk koersgrafiek pakken dan zien we veel ruis, fluctuaties, en omdat wat af te zwakken wordt vaak snel gegrepen naar een gemiddelde (moving average).
U weet dat u uit moet kijken bij het toepassen van een gemiddelde, een verkeerde keuze kan zomaar de signalen van bepaalde golflengte in de koers doen verdwijnen waardoor u dingen ziet die er niet zijn, of juist dingen niet ziet die er wel zijn; meer daarover kan u lezen in het werkstukje:

http://www.jstas.com/Gemiddelden/middelen_maar.htm

Laten we eens gewoon een stukje koersgrafiek pakken.
[b][u]Grafiek 4:[/u][/b]
http://www.jstas.com/Trend2.png

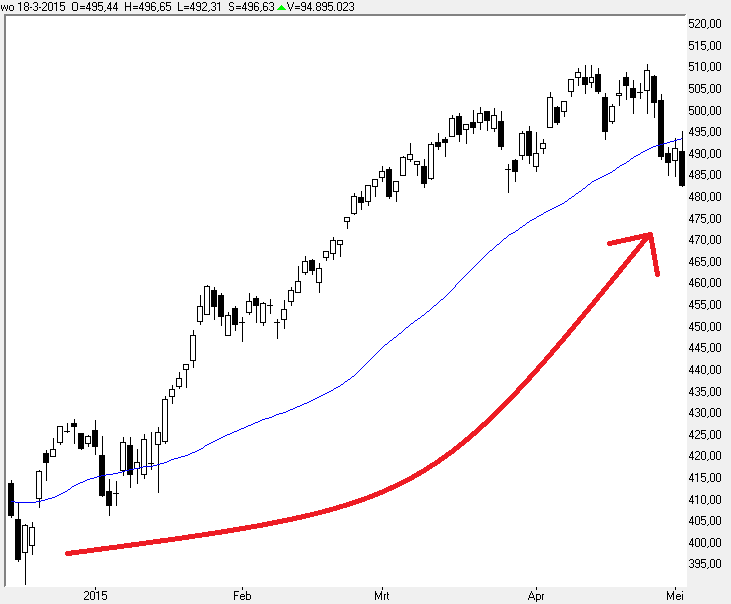
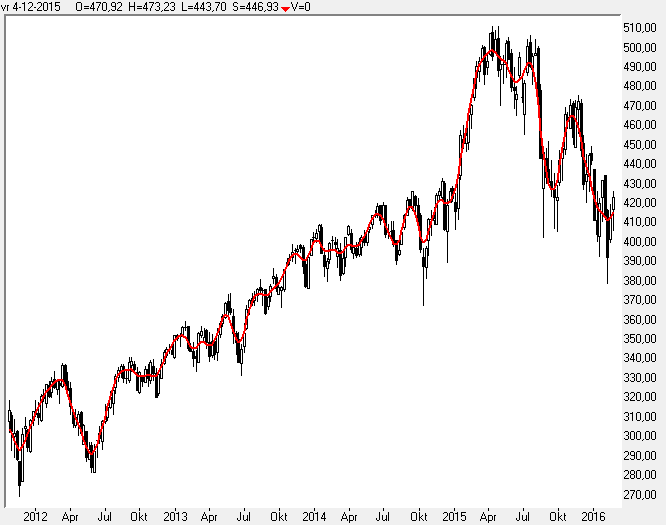
In grafiek 4 ziet u een stukje uit de AEX grafiek, en een ieder zal het er over eens zijn, de trend over het getoonde tijdsbestek is omhoog.
De blauwe lijn is een eenvoudige gemiddelde en die stijgt.
De rode lijn heb ik erin getekend, en u ziet het is feest, de koersen stijgen.
Wie echter eens goed naar de periode eind Maart - begin Mei kijkt ziet toch wel duidelijk dat de koers in die tijd niets is opgeschoten, het uiteindelijke resultaat is een zijwaartse koers beweging.
Het gemiddelde stijgt in die periode echter gewoon lekker door omhoog.
Wat hieruit te concluderen is, is het gegeven dat een gemiddelde niet het geschikte instrument is om een trend aan te geven, immers de koers gaat al een maand zijwaarts en het gemiddelde geeft nog steeds een opgaande trend aan.
Maar wat dan?
Het probleem van een gemiddelde is dat deze door het koersverleden te ver van de huidige koersen af kan komen te liggen (en ik weet wel dat een wma en een ema  dat voor een gedeelte compenseren, maar voor het dramatische effect heb ik even een sma gekozen).
De oplossing voor dit euvel komt vanuit de statistiek.
In de statistiek kent men het begrip lineaire regressie.
Ik zal u niet met de achterliggende berekeningen vermoeien (daarover is in overvloed materiaal aanwezig op het internet) maar kort gezegd komt het op het volgende neer: bij lineaire regressie wordt via de kleinste kwadraten methode een zo goed mogelijk passende lijn berekent over de opgegeven periode.
Kijk, dat klinkt goed in de oren.
Waar een moving average 'last' heeft van koersen uit het verleden, daar berekent de lineaire regressie methode bij elk nieuw element (koersbar) de best passende lijn.
Dus 'geen' na ijlend effect.
Gelukkig heeft elk ta -programma wel een indicator in de gereedschapskist zitten die regressielijn als naam heeft.
Zo ook het programma waarmee ik de volgende grafiek maak, 'Wallstreet For Windows' van Keyword.
Laten we even wat experimenteren met  deze regressielijn indicator.
[b][u]Grafiek 5:[/u][/b]
http://www.jstas.com/trend3.png

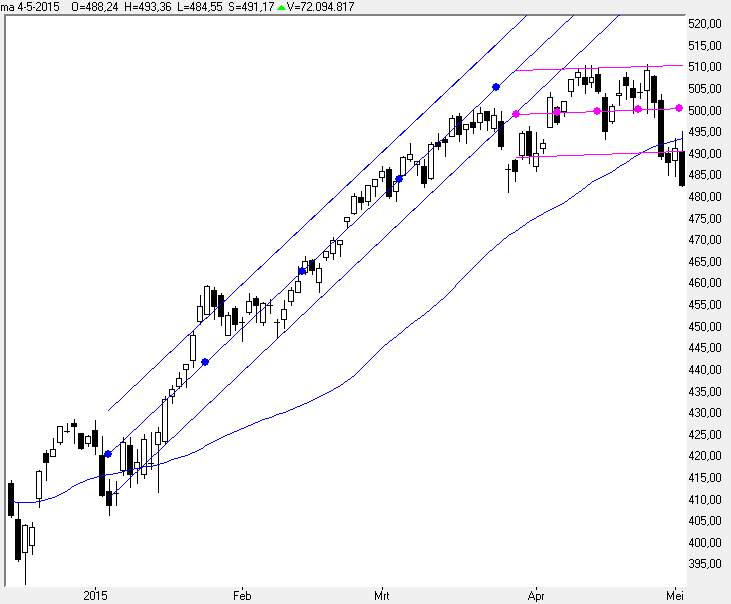
In grafiek 5 ziet u weer een stukje koersgrafiek van de AEX.
De blauwe kronkellijn is dezelfde moving average als in grafiek 4.
De rechte lijnen met de bolletjes zijn de lineaire regressielijnen, terwijl de rechte lijnen erboven en eronder deviatie lijnen zijn.
Ik weet, de tijdvensters verschillen, maar dat doe ik even voor  'het effect'.
De blauw gekleurde lineaire regressielijn geeft keurig de opgaande trend weer, terwijl de paarse lineaire regressie lijn keurig de zijwaartse trend weergeeft, waar de blauwe moving average lijn nog steeds stijgend is.
Kijk, dat biedt mogelijkheden.
Is zo'n regressielijn nu DE oplossing?
Voor dat je wat voor indicator dan ook ergens voor wil gebruiken, moet je je verdiepen in wat hij weergeeft, meet,doet.
Ik heb daarvoor mijn boekje statistiek weer eens uit de motten ballen gehaald en ben onder de motorkap van de regressielijn gedoken.
Ik heb daarna een indicator geschreven (de link naar de code komt aan het einde van dit stukje) zodat we een en ander eens goed kunnen bekijken.
Ik pak grafiek 5 hierboven nog eens, en trek alleen de regressielijn over de maanden Februari -Maart -April van 2015, dus zonder de deviatie banden
[b][u] Grafiek 6:[/u][/b]

http://www.jstas.com/Trend4.png

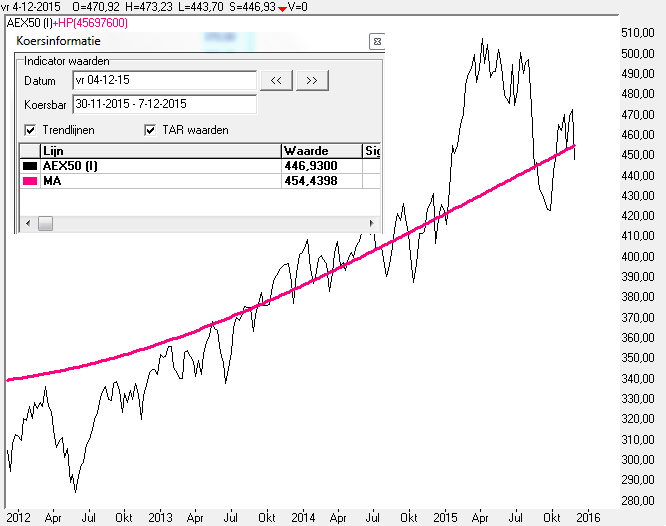
De onderliggende berekening heeft keurig de regressielijn uitgerekend over de periode die de groene lijn aangeeft.
Zo'n berekening begint op de laatste datum, in dit geval 13-April-2015 en rekent dan terug over een bepaalde periode, in dit geval 54 koersbars.
Het einde van de lijn, op 13-04-2015 geeft dus de best mogelijk -fit-  aan rekening houdend met de terugkijk -periode die in idt geval door de groene lijn wordt weergegeven.
We kunnen op 13-04-2015 ook wel een pijltje tekenen aan het einde van deze regressielijn, zoals in grafiek7 hieronder.
[b][u] Grafiek 7:[/u][/b]
[img]http://www.jstas.com/Trend6.png[/img]

U ziet een pijl omhoog, dus deze regressielijn geeft een opgaande trend aan over de gemeten periode. In de onderliggende berekening heeft de helling M in de formule dan ook een positieve waarde.
In onderstaande grafiek ziet u een stukje dalende trend weergegeven waarbij ik de regressielijn weer van een pijltje heb voorzien.
[b][u]Grafiek 8:[/u][/b]
http://www.jstas.com/Trend7.png

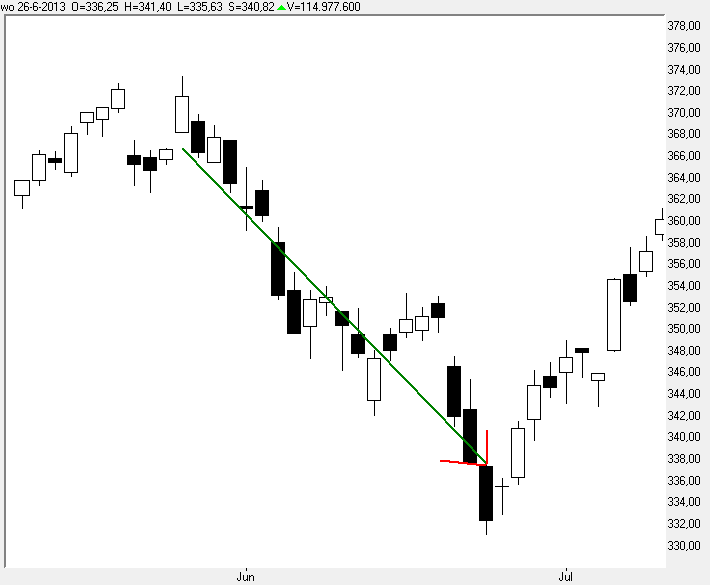
De helling M van deze trend lijn is negatief ofwel dalend.
Zo kunt u zich indenken dat in een zijwaartse trend de regressielijn min of meer horizontaal verloopt, en de helling M zeer gering of nagenoeg 0 zal zijn.
We kunnen voor elk punt van de grafiek de regressielijn berekenen en al deze punten via een lijn met elkaar verbinden (waarbij we de lijn die de lookback periode aangeeft weglaten).
Zo'n lijn zie er als volgt uit.
[b][u]Grafiek 9:[/u][/b]
http://www.jstas.com/Trend8.png

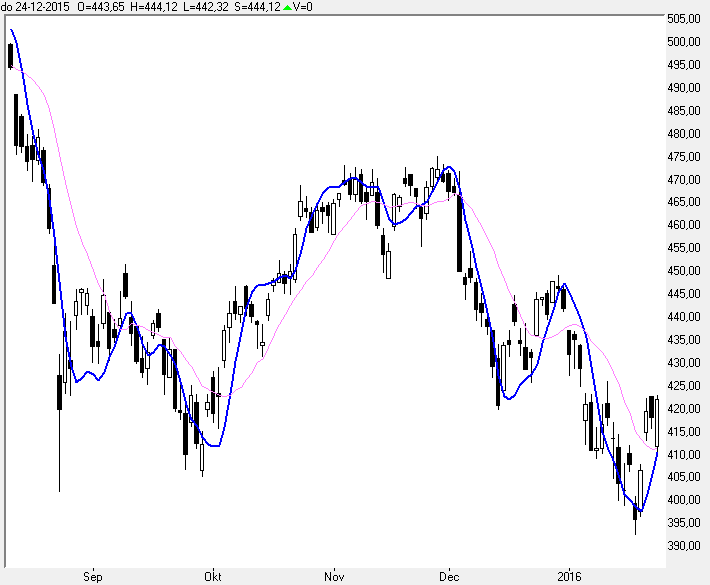
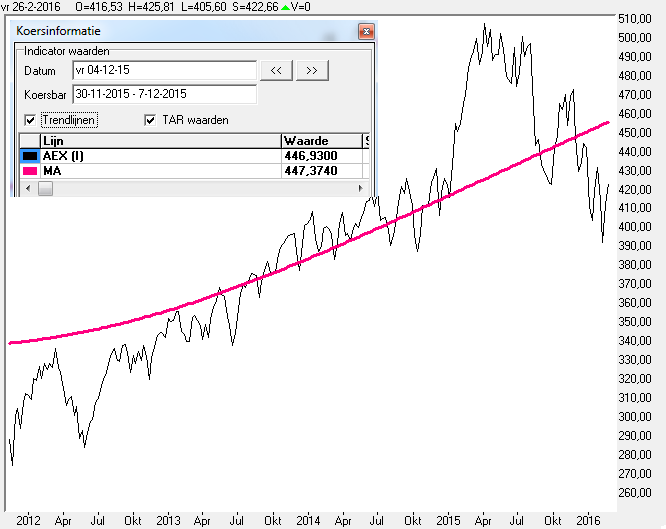
In grafiek 9 ziet u zo'n regressielijn in een blauwe kleur weergegeven met een lookback periode van 13 koersbars.
In de kleur rose heb ik even een MA13 als vergelijk weergegeven, u ziet dat de regressielijn sneller reageert.
Nu is de rose lijn een gemiddelde lijn, maar voor de blauwe regressielijn wil ik niet van een gemiddelde spreken, maar eerder van een Best-Fit-Line.
Hoe -betrouwbaar- is nu zo'n Best-Fit-Line?
De statistiek zou de statistiek niet zijn als men daar geen antwoord op heeft.
In de statistiek gebruikt men daarvoor de term -correlatie-, het verband tussen twee factoren.
Ik pak grafiek 7 nog even terug, maar vervang de koersbars door punten die de slotwaarde aangeven waarop de indicator is berekend.
[u]Grafiek 10:[/u]
http://www.jstas.com/Trend9.png

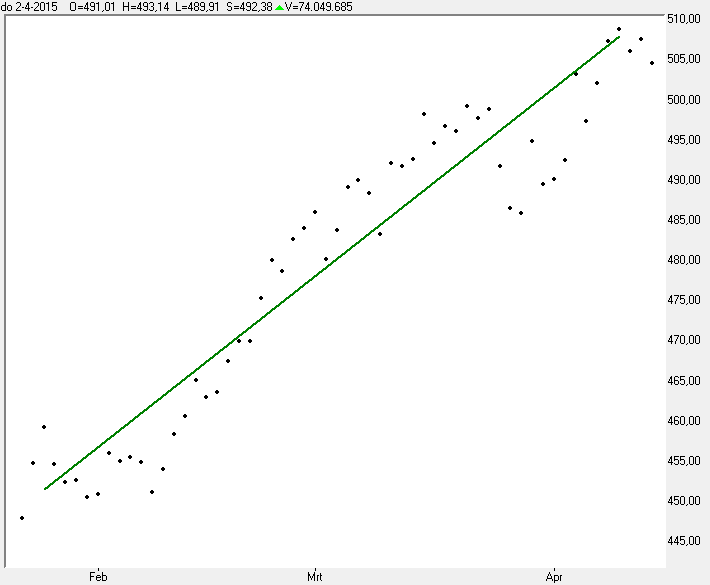
De groene lijn is de regressielijn, waarbij het eindpunt is berekend uit de voorgaande koersen waarbij de lengte van de lijn naar links in de grafiek de periode aangeeft waarover het eindpunt rechts in de grafiek berekend is.
We zien dat de punten als het ware rondom de lijn cirkelen, dus zonder rekenen zien we al wel dat de correlatie hoog is.
Welke correlatie?
Wel, en op dat punt beginnen de nekharen te kriebelen.
We hebben in deze twee dimensionale grafiek slecht twee -variabelen-, en dat is de tijd ofwel de x-as waarbij tijd in dit geval vervangen is door het aantal koersbars; en we hebben de y-as waarop de waarde staat vermeld.
We stellen bij de correlatie berekening dat de y -waarde afhankelijk is van de x -waarde, en daar ligt de oorzaak van mijn nekhaarkriebeltjes, het is immers onzinnig om te denken dat het koersverloop in dit geval afhankelijk zou zijn van de tijd.
Wat we wel kunnen doen is de correlatie berekening gebruiken om te zien in welke mate de regressielijn nog aansluit bij het koersverloop over de gemeten periode.
De berekening van de correlatie tussen koers en tijd in dit geval geeft een waarde welke fluctueert tussen 0 en 1 bij een positieve helling en 0 en -1 bij een negatieve helling.
Bij de waarde 0 is er totaal geen sprake van correlatie en bij de waarde van 1 of -1 is er sprake van 100% correlatie.
Waar ligt de grens van wat nog aanvaardbaar is?
Die grens wordt in de regel gesteld op 0,5 en -0,5
Dus een waarde boven de 0,5 of onder de -0,5 is acceptabel.
In het geschreven stukje code zit  een gedeelte wat de correlatie waarde weergeeft waarbij op 05, en -0,5 een stippellijntje staat weergegeven.
Zodra de correlatie lijn boven de 0,5 of onder de -0,5 staat  wordt de regressielijn als -betrouwbaar-  beschouwt, waarbij -betrouwbaar- moet worden gezien als het gegeven dat de best-fit-lijn redelijk dicht in de buurt van de koers ligt.
Ik ben nogal visueel ingesteld, dus daarom weer even een plaatje, waarbij boven in de grafiek de correlatiewaarde wordt weergegeven.
[b][u]Grafiek 11:[/u][/b]
http://www.jstas.com/Trend10.png

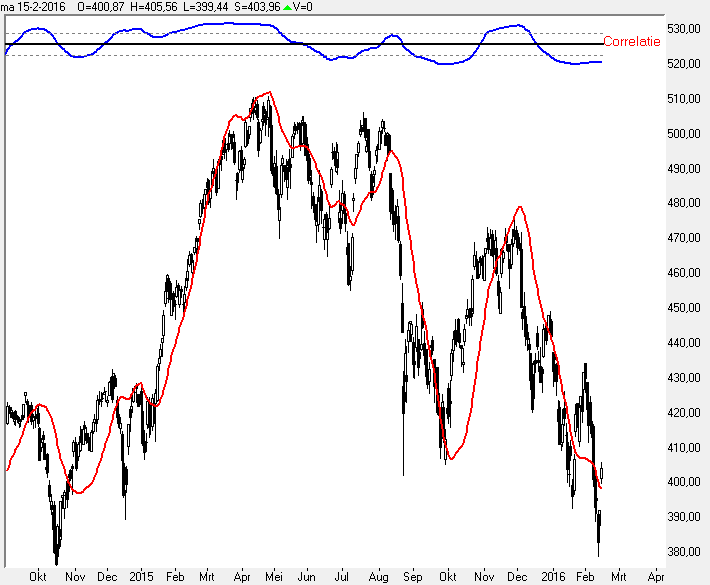
In grafiek 11 hierboven ziet  u in het rood de Best-Fit-Line weergegeven.
Boven in de grafiek heb ik de correlatie waarde weergegeven.
De getrokken zwarte lijn is de nullijn.
De stippellijnen geven de 0,5 en de -0,5  waarde aan.
Boven deze stippellijn is de indicator waarde dus  -betrouwbaar- en onder de stippellijn is de indicator waarde -betrouwbaar- .
Afmeting en plaats van de correlatielijn is instelbaar.
Voor wie liever de correlatiewaarde boven de nul weergegeven wil zien heb ik een instelbaar vinkje meegenomen in de code, waarna bij aanvinken daarvan de grafiek er als volgt uitziet.
[b][u]Grafiek 12:[/u][/b]
http://www.jstas.com/Trend11.png

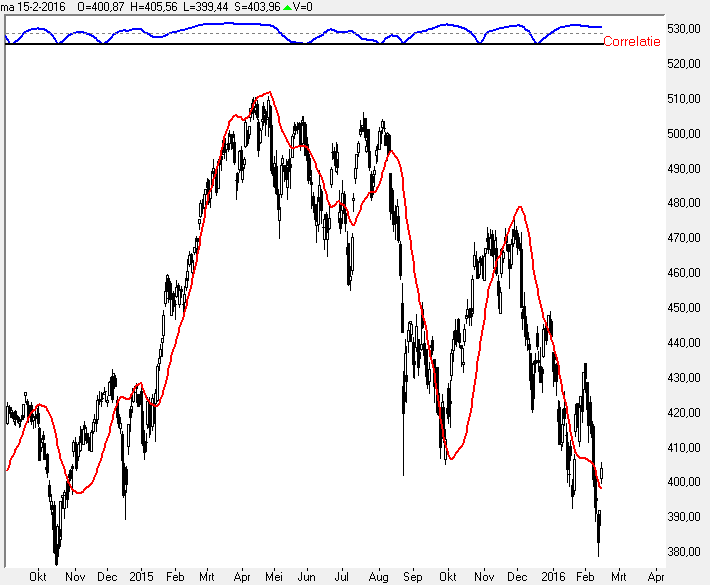
Deze weergave is voor sommigen sneller te overzien.
Ik ben gek op kleurtjes, dus daarom ook even een kleurband in geprogrammeerd, welke ik even onder inde grafiek weergeef, maar plaats en grootte zijn instelbaar.
De rode kleur geeft aan dat er geen correlatie is (gebaseerd op de 0,5 waarde) en volledig groen is aanvaardbare correlatie.
De kleur weergave is ruw, zou kunnen worden verfijnd wanneer dat nodig is.
[b][u]Grafiek 13:[/u][/b]
http://www.jstas.com/Trend12.png

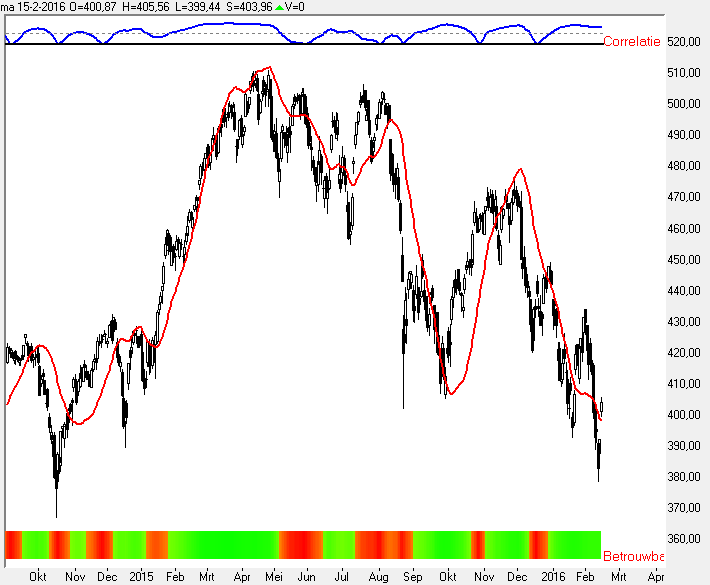
We hebben nu met deze regressie methode een best-fit-line die de trend meet over de opgegeven periode.
We zien dat zo'n lijn sneller reageert dan een gemiddelde lijn (moving average).
Een ieder kent de indicator genaamd Bollinger Bands.
In die indicator worden banden berekend op basis van de Standaard Deviatie en opgeteld -/- afgetrokken van een gemiddelde lijn.
We kunnen dit natuurlijk ook toepassen op deze best-fit-line, zit ook verwerkt in het stukje code.
[b][u]Grafiek 14:[/u][/b]
http://www.jstas.com/Trend13.png

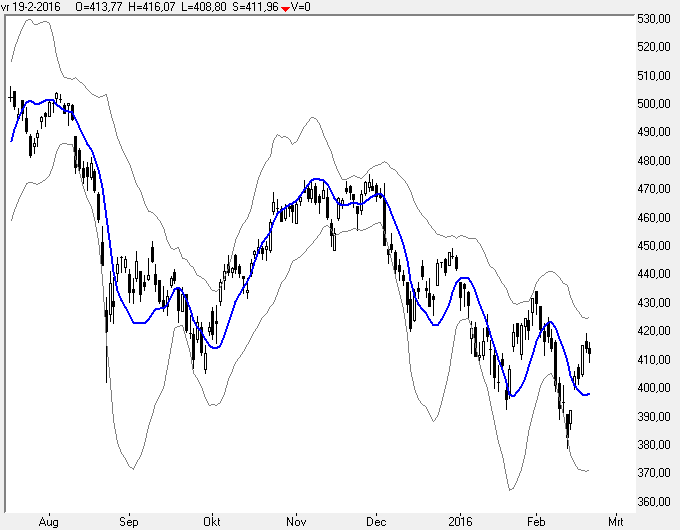
In grafiek 14 ziet u de best-fit-line met daaromheen de standaard deviatie lijnen welke berekend zijn op de slotkoersen van de grafiek.
We kunnen natuurlijk ook de banden berekenen op basis van de best-fit-line, dat ziet u in de volgende grafiek.
[b][u]Grafiek 15:[/u][/b]
http://www.jstas.com/Trend14.png

 
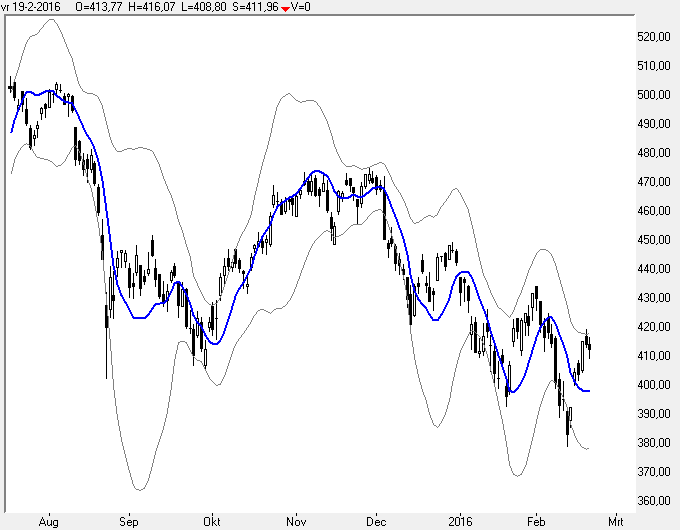
Laten we dit eens vergelijken met de Bollinger Bands indicator.

[b][u]Grafiek 16:[/u][/b]
http://www.jstas.com/Trend15.png

 
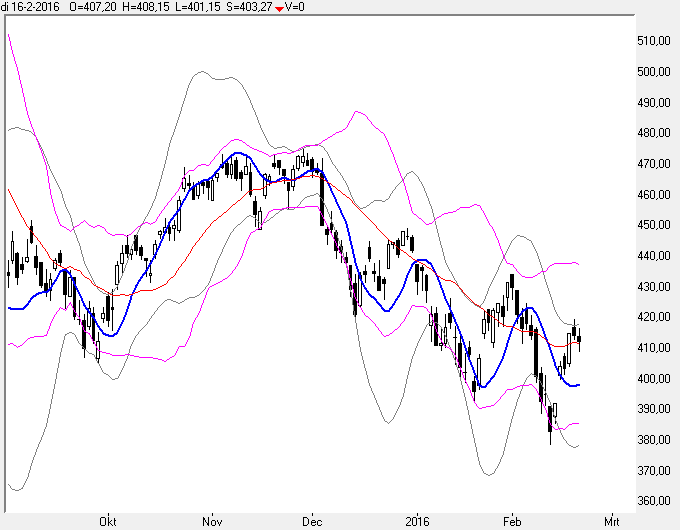
De Bollinger Bands zijn weergegeven via een rode middenlijn en paars gekleurde bandlijnen.
Na handel ikzelf niet direct op de Bollinger  Bands, maar gebruik deze indicator wel voor indicatie (en daar zijn indicatoren dan ook in eerste instantie voor gemaakt).
Laten we even snel een paar puntjes pakken uit het gebruik van de Bollinger Bands indicator.
Eén van de punten is dat wanneer de koers tegen de band aanloopt dat deze van richting wijzigt, maar wanneer de koers buiten de band sluit, dat dit vaak wijst op een verder koers verloop in de richting van de uitbraak.
Ik geef grafiek 16 nog even weer, maar dan met een paar letters erbij.
[b][u]Grafiek 17:[/u][/b]
http://www.jstas.com/Trend16.png

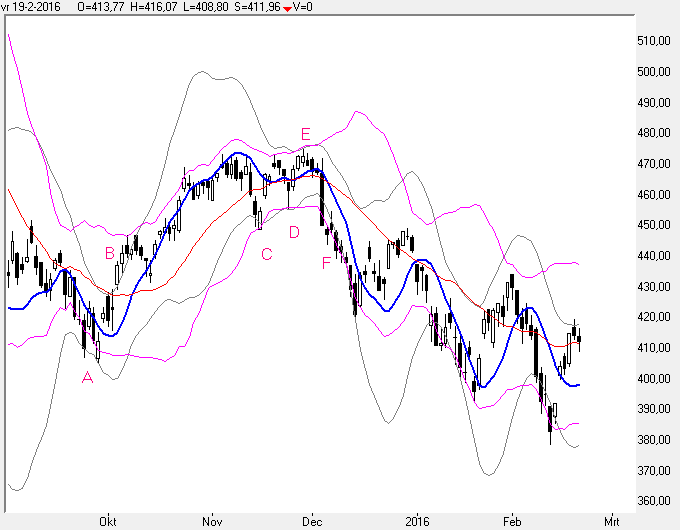
Bij punt A zien we dat de koers afketst op de best-fit-line-band (grijs) waarmee deze wijst op een mogelijk koersomkeer, terwijl de Bollinger-Bands-lijn een doorbraak laat zien en als het ware wijst op een verder dalend koers verloop.
Bij B zien we een uitbraak boven de grijze best-fit-line-band waarmee wordt gewezen naar een verder stijgend koers verloop.
Iets later dan bij B zien we dat de koers lijkt af te ketsen op de Bollinger-bands-lijn waarmee een mogelijke koersomkeer wordt aangegeven.
We zien het verloop erna, na een terugkeer van de koers tot aan de best-fit-line wordt een best stuk verder gestegen.
Bij C,D,E en F zien we dat de Bollinger Bands banden en die van de best-fit-line het aardig met elkaar eens zijn.
Dit komt doordat de gemiddelde lijn van de Bollinger Bands en de best-fit-line op dat moment aardig gelijk op lopen.
Het probleem bij de Bolinger Bands is dan ook het achterlopende gemiddelde.
Zoals u in mijn stukje -Middelen maar- (zie tekst boven grafiek 4) heeft kunnen lezen kunnen we de gemiddelde lijn van de Bollinger Bands opschuiven omdat het achterna ijlen van het gemiddelde bekend is en afhankelijk is van het gebruikte type gemiddelde, maar dan hebben we rechts in de grafiek geen indicatie meer.
Een ander gebruik van de Bollinger Bands is te kijken wanneer de banden zich vernauwen of verwijderen, ik heb daartoe in de indicator een stukje geschreven die de bandbreedte aangeeft.
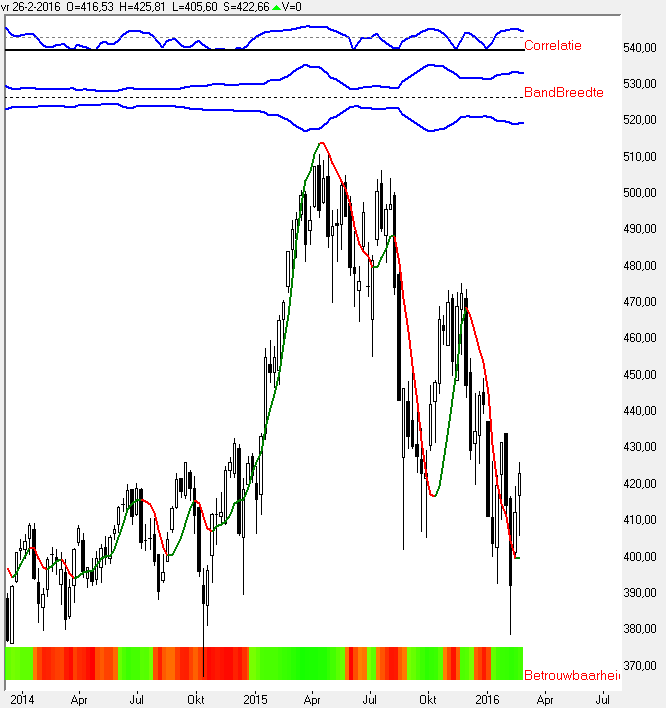
[b][u]Grafiek 18:[/u][/b]
http://www.jstas.com/Trend17.png

Het plaatje spreekt voor zichzelf.
**
De best-fit-line (die dus de richting van de trend probeert aan te geven) ligt dichterbij de koersen dan een gemiddelde lijn, maar heeft ook een na-ijlend effect wat wordt bepaalt door de look-back periode in de formule.
.
Nu is het bepalen van de trend in een data grafiek een probleem wat de onderzoekers al eeuwen bezig houd.
Eén van deze onderzoekers was bijvoorbeeld E.T. Whittaker rond de jaren 23 van de vorige eeuw.
Het werk van Dhr. Whittaker was voor een gedeelte gebaseerd op het werk van E.L. DeForrest uit de jaren 1873-1874 1876.
In de jaren 1980-1997 is dit principe weer verder uitgewerkt door de heren Hodrick en Prescott wat resulteerde in wat nu het HP-filter wordt genoemd.
Het HP filter ontleed de data van de grafiek in trend en cyclus
Het eerste stukje in hun formule zult u herkennen (wanneer u mijn stukje code bekijkt) , het namelijk het stukje wat ook voorkomt in de best-fit-line, en werkt ook op het principe van -de kleinste kwadraten-methode-  zoals toegepast in de regressielijn.
De formule van het HP-filter gaat echter nog een stuk verder, wat zo zijn voordelen oplevert, maar ook enkele nadelen.
Daarover ga ik de volgende keer verder ...
..
Stay tuned ...
.....

Vriendelijke groet,

JanS +'